Assignment 6: PID Controller Theory
Contents
Assignment 6: PID Controller Theory#
The True Value and Error Curves#
The figure below shows a true value curve for a PID controller. Draw the corresponding error curve for this graph. You can draw by hand and upload the picture. (Hint: refer to the error definition equation from before)
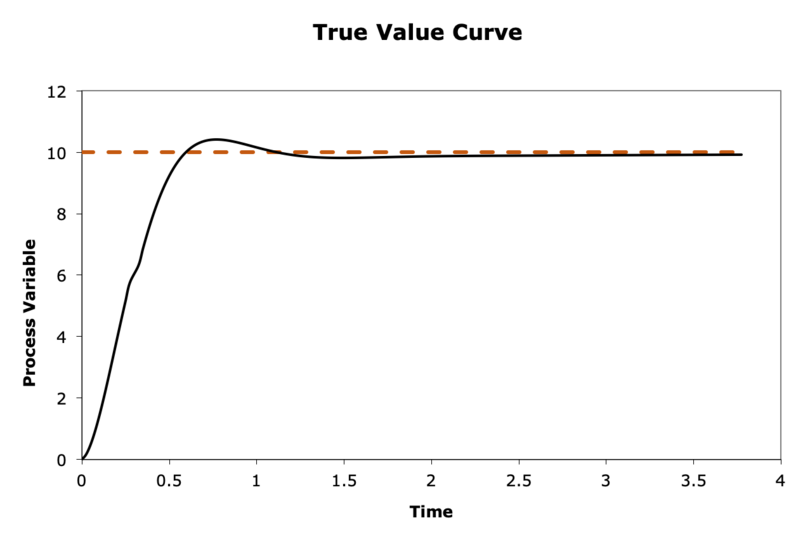
Fig. 10 True Value Curve for A PID Controller. The orange dot line indicates the setpoint and the black line is the true value curve.#
Explain an Effect#
Answer the following questions (3-5 sentences each):
What will happen when the absolute value of \(K_{p}\) is very large? What will happen when the absolute value of \(K_{p}\) is very small?
Can \(K_{p}\) be tuned such that the \(P\) term stops oscillations? Why or why not?
Can the process variable stabilize at the setpoint (i.e. zero steady-state error) with only the \(P\) term and the \(D\) term? Why or why not?
Explain the following effects caused by \(K_{p}\), \(K_{i}\) and \(K_{d}\) (3-5 sentences each). For example, here is a sample answer (though you do not need to follow the pattern):
[Q:] *The rise time decreases when \(K_{d}\) increases.
[A:] *When \(K_{d}\) increases, the error at time step \(t+1\) decreases. This is because larger and larger \(K_{d}\) results in larger and larger control signals at time step \(t\). This drives the system to achieve a lower error at time step \(t+1\). As the error at time step \(t+1\) decreases, the slope of the true value curve increases. Since the slope increases, the rising time towards the setpoint should decrease (slightly).
Start Tuning#
When designing a PID controller, it is important to choose a good set of \(K_{p}\), \(K_{i}\), and \(K_{d}\); poor choices can result in undesirable behavior. The graphs in the figure below illustrate behavior resulting from unknown sets of \(K_{p}\), \(K_{i}\), and \(K_{d}\). In each graph, the orange dot line indicates the setpoint and the black line is the true value curve. For each graph, answer the following (1-2 sentences each):
Which term(s) went wrong, if any? In other words, which term(s) are too high or too low?
How can you correct the behavior?
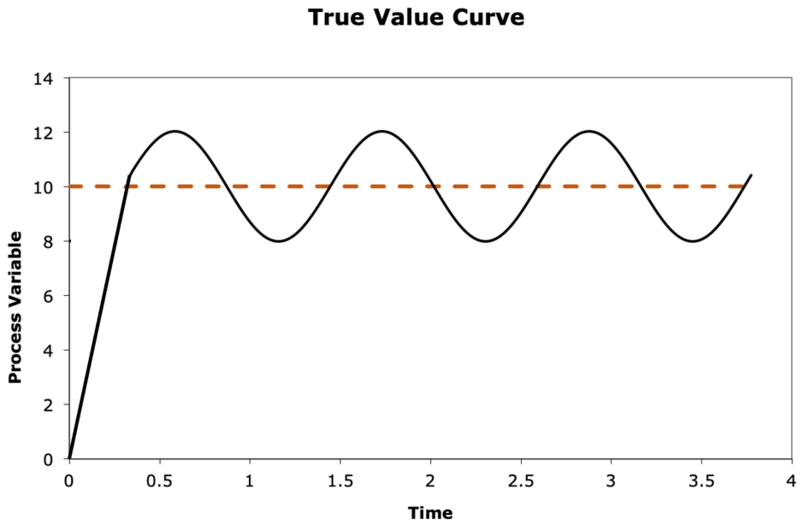
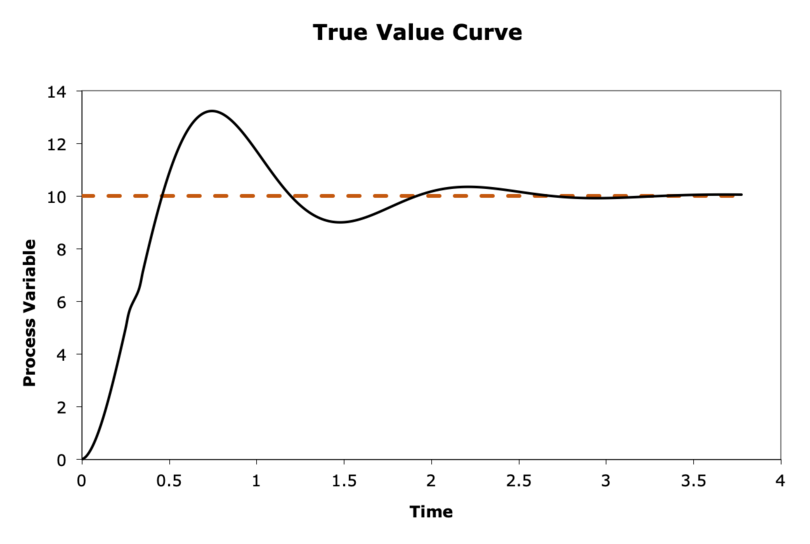
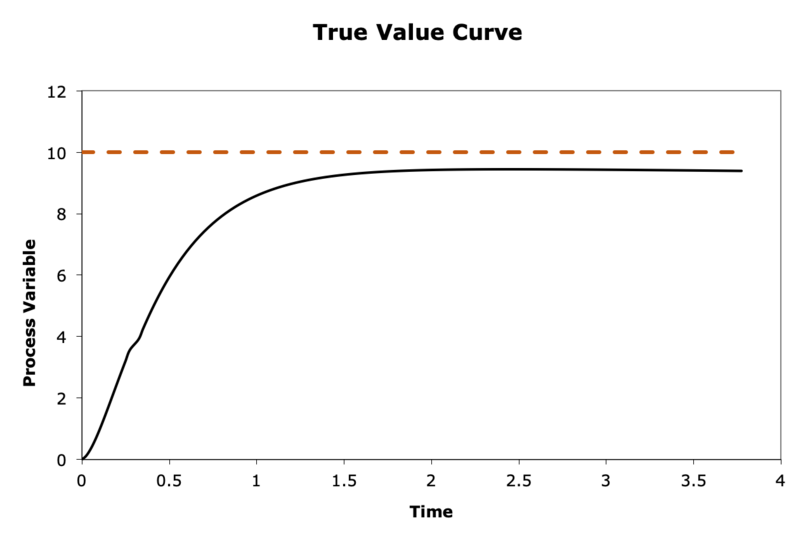

PID on the Duckiedrone#
Sometimes a PID controller will have an extra offset/bias term \(K\) in the control function (see the equation below). For the drone, this \(K\) is the base throttle needed to get the drone off the ground.
Altitude Control#
Suppose you are implementing an altitude PID controller for your drone (i.e. up/down movement).
If the setpoint is the desired height of the drone, then what is the process variable, the error and the control variable for the altitude PID controller?
What could happen if \(K\) is set too high?
Note: We are looking only for a higher level description to demonstrate understanding of the PID controllers.
Velocity Control#
Suppose you are implementing a velocity PID controller for your drone. In this case, the drone only moves forward/backward and left/right. Your (hypothetical) controller is implemented so that when ‘L’ is pressed, the drone moves left at a constant velocity, and when ‘L’ is released, the drone stops moving.
What is the setpoint, process variable, error and control variable for the velocity PID controller?
How do these key terms change to cause the drone to move when you press ‘L’?
Note: We are looking only for a higher level description to demonstrate understanding of the PID controllers.

