Part 3: Gimbal Lock

The orientation of an object in 3D space can be described by a set of three values: \((\alpha, \beta, \gamma)\), where \(\alpha\) is roll, \(\beta\) is pitch, and \(\gamma\) is yaw.

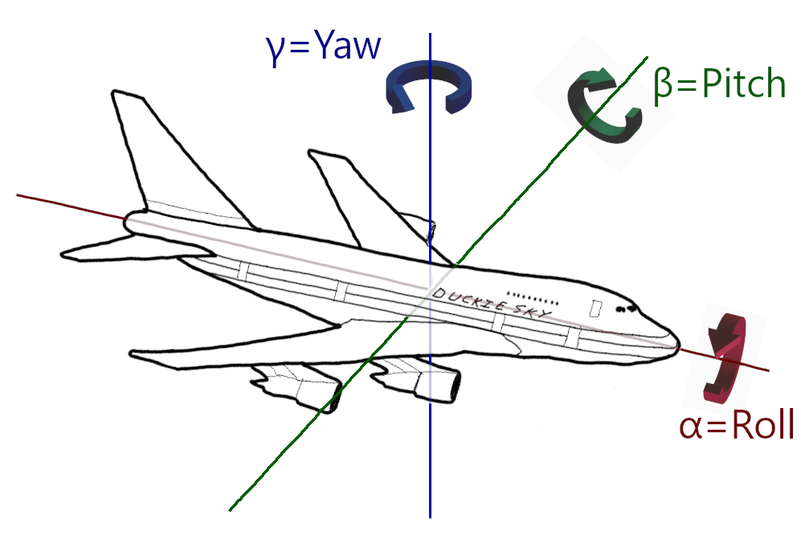
Fig. 4 Roll, pitch, and yaw

Mathematically, any point \(\mathbf{p}\) on an object that undergoes rotation \((\alpha, \beta, \gamma)\) will have a new coordinate \(\mathbf{p'}\) calculated as follows:

\[ \mathbf{p'} = R \mathbf{p} \]

Where:

\[\begin{split} \begin{align*} \mathbf{p'} &= \begin{bmatrix} x' \\ y' \\ z' \\ \end{bmatrix} \\ R &= \begin{bmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \\ \end{bmatrix} \\ \mathbf{p} &= \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} \end{align*} \end{split}\]

Gimbal Lock

Ideally, we would hope that the parameters \((\alpha, \beta, \gamma)\) are enough to rotate any point \(\mathbf{p}\) (distance \(d\) from the origin) to any other point \(\mathbf{p'}\) (also distance \(d\) from the origin, since rotations do not change distance). Upon closer thought, it would seem as if we have more than enough parameters to do this, since it only takes two parameters \((\theta, \phi)\) to describe all points on the 3D unit sphere

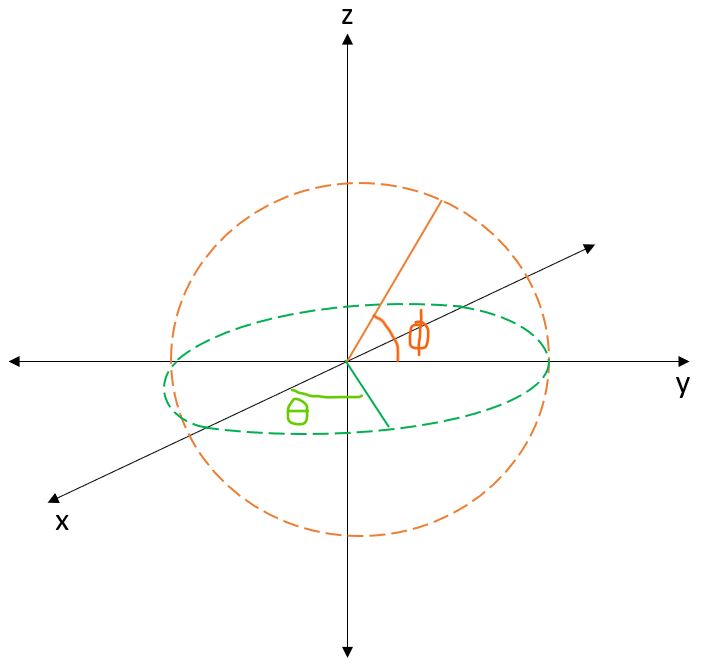
Fig. 5 Two parameters sweeping out a sphere

However, this intuition is a bit off. If any one parameter is held fixed, it may be impossible for \(\mathbf{p}\) to be rotated to some other \(\mathbf{p'}\) by varying the remaining two parameters. Moreover, if a certain parameter is set to a certain problematic value, then varying the remaining two parameters will either sweep out a circle (not a sphere!), or not affect \(\mathbf{p}\) at all, depending on what \(\mathbf{p}\) is. This result is way different from what we expected! The name for this degenerate case is gimbal lock.

Questions

1. Suppose an airplane pitches the nose up to a pitch of \(-\pi / 2\) (\(90 \degree\) up):

   

   Fig. 6 Airplane

   

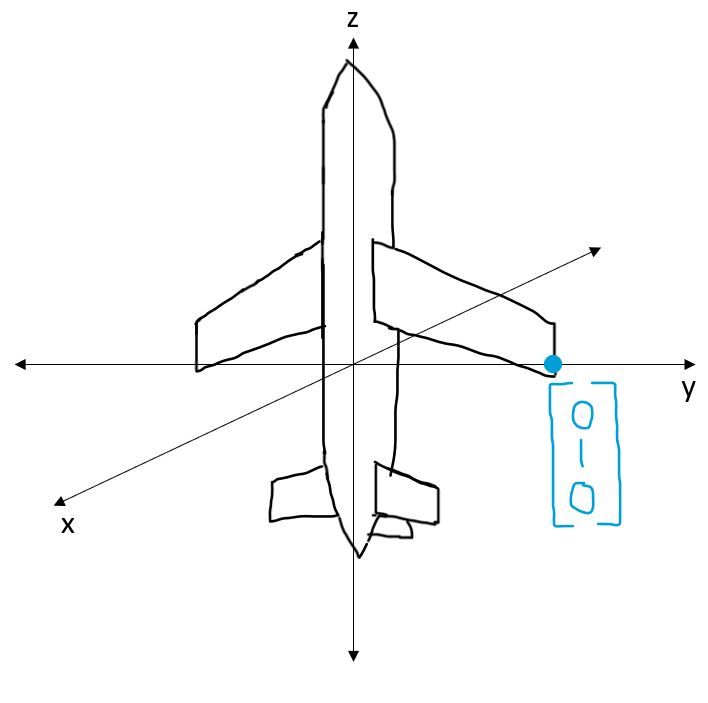
   Fig. 7 Airplane with pitch at 90 degrees

   Let \(R_{\text{gim} \beta}\) denote the rotation matrix \(R\) for \(\beta = -\pi / 2\). Prove that

   \[\begin{split} R_{\text{gim} \beta} = \begin{bmatrix} 0 & -\sin(\alpha+\gamma) & -\cos(\alpha+\gamma) \\ 0 & \cos(\alpha+\gamma) & -\sin(\alpha+\gamma) \\ 1 & 0 & 0 \end{bmatrix} \end{split}\]

2. Consider the point \(\mathbf{p} = [0 \quad 1 \quad 0]^T\) on the pitched airplane, i.e. the tip of the wing. Does there exist any \(\alpha, \gamma\) such that \(\mathbf{p'} = R_{\text{gim} \beta} \mathbf{p}\) for \(\mathbf{p'} = [1 \quad 0 \quad 0]^T\)?

   Show your work and briefly explain your reasoning (1-2 sentences).

3. Consider the point \(\mathbf{p} = [0 \quad 1 \quad 0]^T\) on the pitched airplane, i.e. the tip of the wing: Can we set \(\alpha, \gamma\) such that:

   \[ \mathbf{p'} = R_{\text{gim} \beta} \mathbf{p} \]

   for some \(\mathbf{p'}\) on the XY unit circle (e.g. \([\frac{\sqrt 2}{2} \quad \frac{\sqrt 2}{2} \quad 0]^T\))?

   You do not have to show any work, but briefly explain your reasoning (1-2 sentences).

4. Consider the point \(\mathbf{p} = [0 \quad 1 \quad 0]^T\) on the pitched airplane, i.e. the tip of the wing. Can we set \(\alpha, \gamma\) such that:

   \[ \mathbf{p'} = R_{\text{gim} \beta} \mathbf{p} \]

   for some \(\mathbf{p'}\) on the YZ unit circle (e.g. \([0 \quad \frac{\sqrt 2}{2} \quad \frac{\sqrt 2}{2}]^T\))?

   You do not have to show any work, but briefly explain your reasoning (1-2 sentences).

Reflect on your answers to the previous 4 questions. What are the questions trying to portray? Why are the answers different? Why is \(-\pi / 2\) (i.e. pitched up \(90\degree\)) a “certain problematic value”? What would happen to an airplane that pitched that much? Could a pilot recover from such a situation? Are 3 parameters enough to allow for rotations in all situations?